Hi iMaterialise fans,
Iwahswap is the world’s first truly hyper-exponential puzzle. That is, whenever the puzzle is expanded with one extra piece, the number of moves grows with a factor, and that factor increases with the number of pieces. The puzzle was developed in a creative exchange between Iwahiro (Hirokazu Iwasawa), Goetz Schwandtner, Bram Cohen and myself. The breakthrough idea came from Iwahiro, who suggested to look into the Steinhaus–Johnson–Trotter algorithm. That algorithm itself turned out to be too complex to implement mechanically, but Iwahiro found a simplification that was still hyper-exponential. Then I found a solution to implement it mechanically.
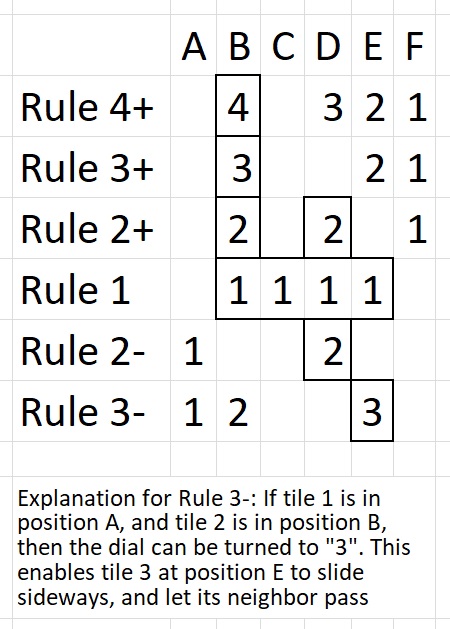
The puzzle has five tiles that need to change order, from 12345 to 54321. The mechanism with the gray slider enforces that only neighboring tiles can be swapped (cf bubblesort). The dial above the tiles tells which tile can slide to the right, for swapping with a higher-numbered tile. The dial can be turned to a number if all numbers below are in order at one of the ends.
Below is a table of the minimum number of moves to solve. One can easily verify that the puzzle is hyper-exponential. The original prototype used six tiles. However, that took way too many moves (273) to solve. Hence the five-tile version is prefered (48 moves).
Watch the YouTube video.
Download the CAD file to print-it-yourself.
Buy the puzzle at my iMaterialise Shop.
Read more at the Non-Twisty Puzzles Forum.
Check out the photos below.
Enjoy!
Oskar
Tiles: moves
2: 1
3: 3
4: 12
5: 48
6: 273
7: 1623
8: 12648
9: 100848
10: 993873
11: 9924123
12: 117980148
13: 1414652448
14: 19676120673
15: 275336675823
16: 4384167026448
17: 70125452636448
18: 1257577423967070
19: 22631712907918300
20: 451301874558273000